Collatz Conjecture: Math, Data Visualization, and Music… Blocks
This article details how I used Music Blocks to express the Collatz Conjecture. I describe what the conjecture is, why I chose it, and what it has to do with music. I also share my work thus far and encourage readers to try different extensions of my project–either on their own or together with their students in the classroom. All-in-all, I find it exciting that Music Blocks can be used in such a way to explore math, data visualization, and music.
My Inspiration
Last week I was reading a wonderful article that criticizes the standard approach to math education in the United States. The article is called “A Mathematician’s Lament” and is written by mathematician Paul Lockhart. I encourage you to read it, and I plan to write more about it in the coming months. The basic gist of the article is that students are never given real “problems” to solve in math classes.
Mathematics is the music of reason. To do mathematics is to engage in an act of discovery and conjecture, intuition and inspiration; to be in a state of confusion— not because it makes no sense to you, but because you gave it sense and you still don’t understand what your creation is up to […]
A Mathematician’s Lament, Paul Lockhart
In the spirit of this article, I decided to give myself a real problem to solve. I decided to express the Collatz Conjecture in Music Blocks. What I ended up with is a fanciful program that helps one to visualize the data output of the Collatz Conjecture musically.
What is the Collatz Conjecture?
[S]tart with any positive integer n. Then each term is obtained from the previous term as follows: if the previous term is even, the next term is one half of the previous term. If the previous term is odd, the next term is 3 times the previous term plus 1. The conjecture is that no matter what value of n, the sequence will always reach 1.
Definition of Collatz Conjecture as described on https://en.wikipedia.org/wiki/Collatz_conjecture
The Collatz Conjecture is an unproven mathematical assumption that says that for any positive whole number you put it into the following algorithm and you will always end up with a loop of 4, 2, and 1:
- If the number is even, divide by two.
- If the number is odd, multiply by three and add one.
As you can see, the basic math is very simple. However, the beauty of the conjecture is that it takes a lot of imagination to prove that it will absolutely always end up with the same numbers. There could be, for example, a theoretical high number, that would never return to 4, 2, and 1. For all the numbers that have been tested thus far, including by super computers, the same results have been arrived.
Why the Collatz Conjecture?
I chose the Collatz Conjecture because Musician and Mathematician Rob Flax got me excited about it, and even has a very cool piece of music that uses certain inputs to the algorithm to inspire the overall form of his piece. I also chose the Collatz Conjecture because its pseudo-randomness makes it ripe for interesting musical results.
Certain numbers generate certain patterns that provide interesting and unexpected results. Since an odd number result will result in a higher number and an even number will result in a lower number, the results can often bounce around, up-and-down in somewhat unpredictable ways. I was curious to hear what this sort of pattern could sound like, and Music Blocks is a very good tool for doing so.
My Project: Math, Data Visualization, and Music
To be honest, I was not entirely confident that I had the programming and computation chops to express the Collatz Conjecture with Music Blocks. In fact, I have thought of doing such a project a few times before, and have made some attempts, but failed. This time, however, excited about the “math as art” approach suggested by the Lockhart article, I decided to take the dive once again.
I focused on the process, not as much on the outcome. I focused on creative choices, not on mathematical rules. With my head clear of these smaller issues, I began a new project and started solving the smaller problems in order to get closer to my main goal.

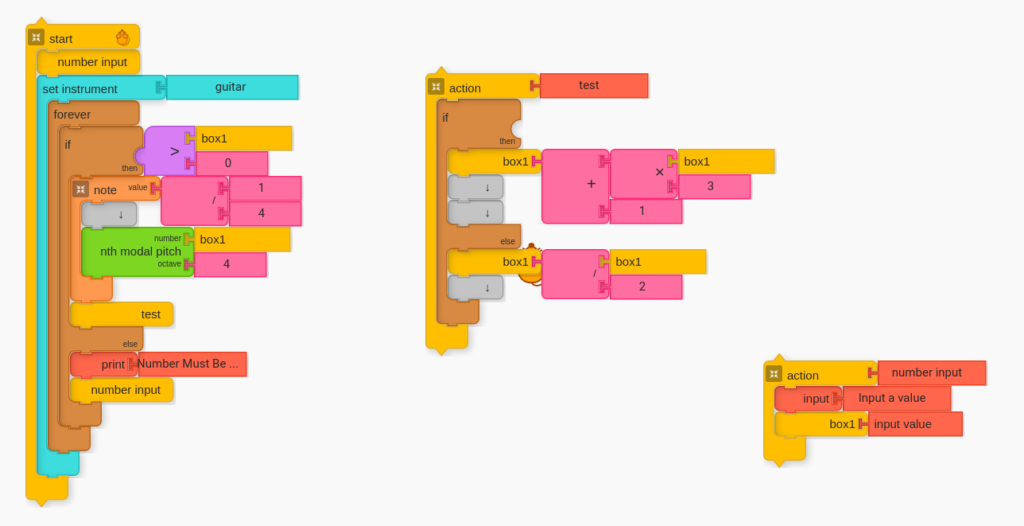
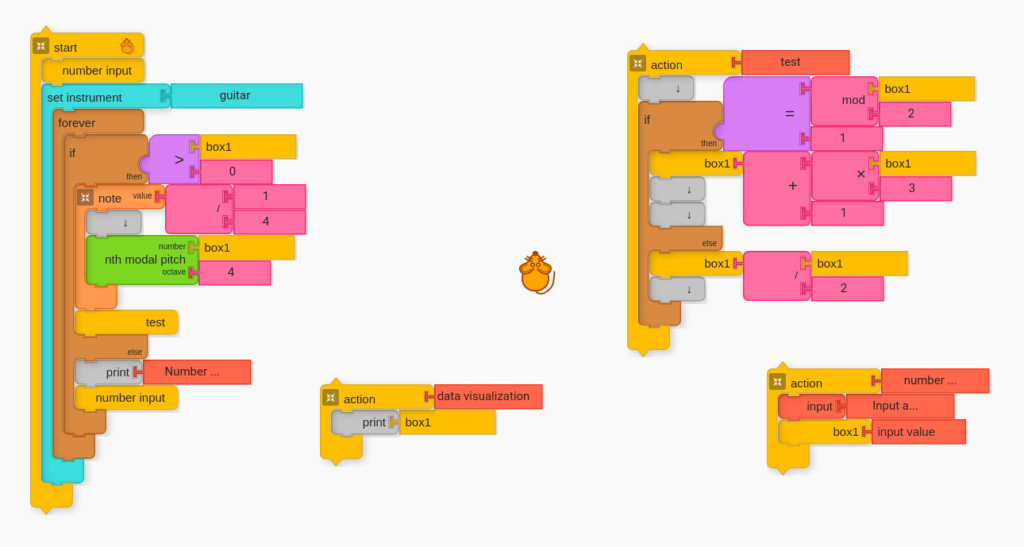
Half-Finished Code. Trying to Figure out How to Determine Odd and Even. 
Main Algorithm of Collatz Conjecture 
Adding Data Visualization as a Feature.
Whenever I got stuck, I employed a technique that I have found very helpful in problem solving. I have been inserting undefined (i.e. empty) Action blocks and naming them what I want them to do when I am done. Doing things this way allowed me to focus on the big picture rather than get stuck on any particular part of my code. It also allowed me to work non-linearly. So if I was not yet ready to figure out some problem near the beginning of my script, I could work on another spot.
Completed Project
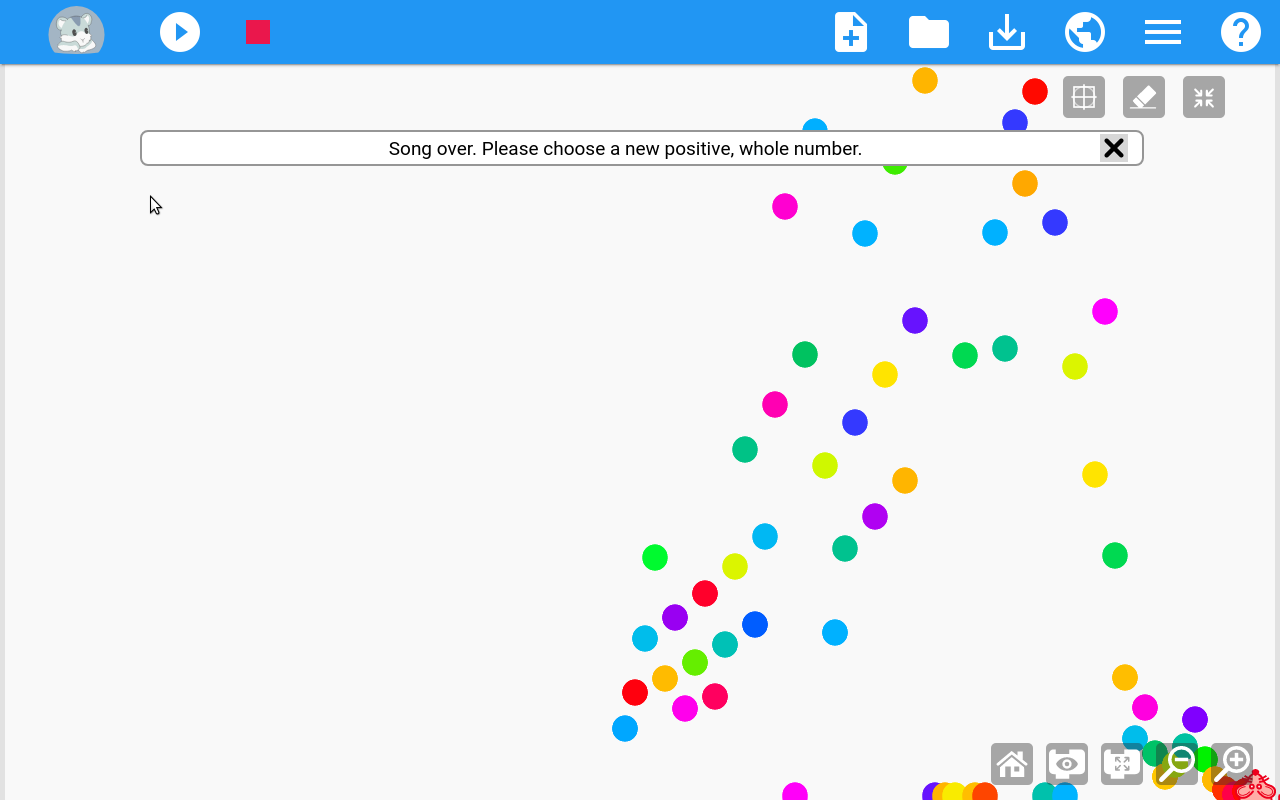
The completed projected is a lot of fun. You can put any number in and get a musical result. Check out the video and the link below.
Try the Collatz Conjecture Project at https://musicblocks.sugarlabs.org/index.html?id=1631387944016609&run=True
A Side Note About Visualizing Data as Sound: Data “Auralization”
When writing this article, I found very narrow definitions of the term “data visualization“. In my mind, auralizing data through sound is a perfectly natural thing to do. However, most definitions focus solely on the “visual”. It is interesting to imagine how Music Blocks may be used to help us carve new paths for understanding data/information.
A quick search about “data auralization did return a few articles worthy of interest. AURALIZATION: Representing Data as Sound by Buxton, Gaver & Bly, for example, is worth looking at.
Visualizing Sound
Just to pull everything “full circle”, let’s not forget that you can still visualize sound. Using Music Blocks’ “Save as Lilypond” feature, I exported sheet music for original input of “71”. The following PDF is the sheet music. I encourage you to try it on an instrument, such as guitar or piano. (BTW, if you ever get bored of practicing scales, I highly recommend integrating something like this into your practice routine. Cheers!)
Editorial Note: Due to a bug in how Music Blocks annotates Lilypond sheet music, the numbers above the notes are offset by one note. The first note (i.e. pitch of d) should have “71” above it (mod14 of 71 = 1), the second note (i.e. pitch of g) should have “214” above it (mod14 of 214 = 4), etc.
Extensions and Next Steps
The program I created is fairly robust in a number of ways. It checks to make sure that the user is inputting a positive whole number. Negative numbers are rejected and the user is asked to input a new number. Numbers with decimal places are automatically rounded. I even made sure that the final 4, 2, 1, loop only happens a few iterations before the user is prompted to input a new number. Without this final part of the code, the program would need to be stopped and run again for a user to try unique numbers.
TODO: More Refined Artistic Choices
Next steps could be something like this: I made very simple artistic choices for this first draft. For example, the rhythm is monotonous. There is no variety in the rhythm whatsoever. Some (higher) pitches do pop out, which makes it sound somewhat more rhythmic. But not much thought was given to this dimension. Another next step could be to try a different range of pitches. I confine the pitches to two octaves by using “mode length” multiplied by two for the “mod space”. However, a higher multiple could be tried. Also, I am not even sure this is the most meaningful choice. What range would be the most meaningful, and produce the most interesting sound? Different scales/modes could also be chosen based on preference.
Your Move: Remix and Share your Project on this Blog
There is still so much that can be done with a project such as this. My project is merely the starting point. Other teachers and students are encouraged to make their own remixes. What improvements might you make? What artistic choices would you make, and what experiments would you try? I encourage anyone reading this to give it a try.
In the spirit of giving problems not answers (which is a main theme in the Lockhart article), I am purposely leaving some room for improvement. I will continue to improve my program, for sure. However, I challenge you to try my program (linked above) and contribute your own artistic choices. Once you have something to share, please contribute a blogpost about your project. Cheers!
Conclusions
I found it to be very fun to attempt to express an interesting mathematical idea with Music Blocks. The Collatz Conjecture is a novel problem still awaiting a solution. (In fact, since Music Blocks–and the entire idea of “coding music”–is so new there are many unsolved problems waiting for students and teachers to solve.)
My project, of course, does not prove the conjecture, but it did get me one step closer to understanding the problem. It also allows me to visualize the data musically. There are many visualizations for this conjecture that are purely graphical. Graphical is very important, but a musical visualization can open new doors as well. In some ways, I found that I could feel the patterns better musically than with graphs. It also seems to me that musical data visualization could be, in many ways, more efficient.
Imagine a world where for a meeting, information was not just presented graphically on a whiteboard, but also converted to music? This is one of the directions that is possible when you explore music and coding.
And, who knows? Perhaps the solution to proving (or disproving) the Collatz Conjecture has been lying under our ears all along! If you do get some novel insight about the conjecture, please share in the comments below.












Here is a great video I found that explains the Collatz Conjecture. https://invidio.us/watch?v=094y1Z2wpJg (Invidious allows you to watch videos hosted on YouTube in freedom and privacy. Follow any of the links to watch.)
We already got an awesome remix of this project. Created by microtonalist Kite Giedraitis is a microtonal remix of the Collatz Conjecture project. You can try it for yourself at https://musicblocks.sugarlabs.org/index.html?id=1631608560267533&run=True
I went ahead and made a remix to Kite’s remix. Check it out at https://musicblocks.sugarlabs.org/index.html?id=1631720223522003&run=True | It has some checks for very high and low numbers, as well as scrolling the canvas over time so that you can see the order of the pitches over time.