Experimenting with Fibonacci
The Fibonacci Sequence is a numeric set that has quite the history. Created by Fibonacci, the sequence is well-known for its usefulness in creating art and architecture of beauty. You may have heard of The Golden Ratio, which is intimately connected to the Fibonacci Sequence. There is much to reference for the connection between Fibonacci Sequence to visual art and architecture.
However, what the Fibonacci series sounds like? This is the question that Walter Bender, Rob Flax, and I explored recently in preparing for an upcoming “Pi Day Concert” hosted by MAP Family Learning Center (see this page for more info and registration).
Origins of our Latest Creations
Walter Bender and I have been experimenting with Fibonacci and Music Blocks since its beginnings. For example, Walter Bender remixed a Turtle Blocks project based on the Fibonacci Sequence called “Musical Nautilus” (Run Project). Just recently, in an effort to create something new for the upcoming P Day concert, we experimented by remixing the “Musical Nautilus” piece in a way where semitones pitches are mapped to the Fibonacci Sequence in mod-12 space. Check it out at https://musicblocks.sugarlabs.org/index.html?id=1614295906967854&run=True

Walter, Devin, and Rob Flax meeting and discussing ideas 
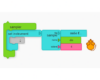
One of the first results of our “Fibonacci Music and Mod-12” 
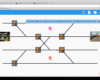
Visual Output from Fibonacci Experiment (More Flourished)
What we Learned
What did we learn from our mod-12 Fibonacci Music? Well, for one, we found another way to love the Fibonacci Sequence, because we found the sound of the resulting melody to be very satisfying. We also learned a few properties of the resulting melody. For example, it is very interesting that there of all the 12 possible chromatic pitches, 6 is skipped. In a twelve-pitch series starting from 0, this would be the tritone, which is the tone that is directly in the middle of the octave. It is also very dissonant and highly unstable. At one point in history, in fact, the tritone was known as the “Devil’s Interval“. It is interesting that this particular pitch, out of all of the twelve options, is the one that is skipped.
What are the Fibonacci Numbers in a Mod-12 Space?
a(n) = Fibonacci(n) mod 12
0, 1, 1, 2, 3, 5, 8, 1, 9, 10, 7, 5, 0, 5, 5, 10, 3, 1, 4, 5, 9, 2, 11, 1Note: This pattern repeats after the 24th number (all 24 listed above), and it repeats forever.
Reference: https://oeis.org/A089911
Fun Challenge! Find a fretted instrument (e.g. guitar/ukulele/mandolin/etc) and play the above sequence of numbers as frets (1 as “first fret”, 2 as “second fret”, 0 as “open”). What do you think of the sound? Does it inspire any interesting new musical ideas?
What do these Numbers look like in Musical Notation?
What does this sound like on an Real Instrument?
Yesterday, I did a little experiment with the Fibonacci Sequence on my guitar that you can hear at https://media.publit.io/file/2021-02-25-161255.html Basically, I tried to accompany all of the pitches in the Fibonacci Sequence with major chords.
Note: I started from the 24th pitch of the sequence, B. It sounds a little bit like we are it the key of C (Major?), and the B functions a bit like the leading tone. The first B sounds a little bit like a “pickup”, an anacrusis, to the pattern.)
That being said, this recording is just a crude start. Rob and I plan to polish this out over the coming weeks and create something satisfying for the Pi Day concert. We hope to see you there.
Reading this after the concert has already passed? No worries. I plan to publish the recording of the concert. Moreover, experimenting with Math and Music is always an ongoing project, and that is why we have tools like Music Blocks. Enjoy, and stay tuned via our newsletter!